当サイトではアフィリエイト広告を利用しています。
おさえておきたい寸法計算
Tomix レールを活用してオリジナルのレイアウトを作りたいと思った時に
役立つ寸法計算について紹介します。
さまざまなレールが用意されている中で、独自のレイアウトを作ろうとした時に難しいのがカーブレールの扱いだと思います。楕円なら左右上下対称で分かりやすいですが、45度カーブさせて直線レールいれるとどうすれば一周つながるんだろうとか。そんな時に自分でサイズを計算できると良いですよね。この記事では寸法を計算する方法を解説します。
カーブレールをいれることでどのくらいの長さになるのか? Tomix の標準的なレイアウトとして紹介されているレールの利用方法を見てみたいと思います。
たとえば Tomix の半径 541mm、15度のレール。標準的な分岐ポイント (PR541-15 / PL541-15) やそれと組み合わせて使うカーブレール (C541-15) の規格です。
Tomix レールでレイアウトを組まれている方なら、複線間隔 37mm で分岐させたり渡り線で活用できたりするのをよく御存知かと思います。

では、これを実際に計算してみると複線間隔 37mm となるでしょうか?あるいは長さは 140mm になるのでしょうか。
必要なのは三角関数。中学校でみなさん習ったと思います。
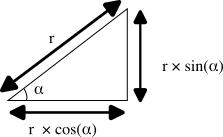
これですね。三角形の辺の長さを計算するやつ。左右反転させても同じです。コレを覚えておけばカーブレールを使った時の寸法計算は可能です。
上の図で言う r が半径 541mm、角度αが 15度の時、このときの計算ができれば求められそうです。
三角関数対応の電卓なんてもってないよー、電卓ソフトどう使えば良いの?って思われるかもしれませんが、実は Google で検索条件入れるところに 541 x cos15度 って入れて検索してみてください。かけ算記号はアルファベットの x で大丈夫みたいです。
電卓が表示されて、522.565872022 と計算結果が表示されたのではないでしょうか。そう、なんとこんなところでも Google 活用できるんですね。便利です。もちろん電卓ソフト使える方はそれでも OK です。
ちなみに、角度は “度” をつけてあげないとラジアンとみなされるので気をつけましょう。

上の図の赤い辺の長さが 541× cos (15) ですので、541 から赤い辺の長さを引き算して 約 18.5mm がポイントのカーブ側の分岐により、図で言うと下側にずれることが分かります。
※この記事では簡易的に sin (α) や cos (α) の アルファの角度は単位:度 (degree) とします。
そして、平行になるように C541-15 を入れますが、こちらも全く同じ半径、角度ですので、同じだけ下側にずれることになります。つまり約 18.5 の2倍、37mm 下側にずれることが分かります。
正確に言うと、18.43… の2倍なので少し 37mm には足らないですが、1mm 程度は誤差として許容できることになります。

上図のように、ポイントとカーブレールの間に S140 を一本はさむと、さらに 140× sin (15) 、つまり約36.23mm 下側にずらせます。これも 37mm とみなして、複線間隔を標準の2倍の 74mm に変更できます。
140× sin(15) で計算できるのは下図の通りです。
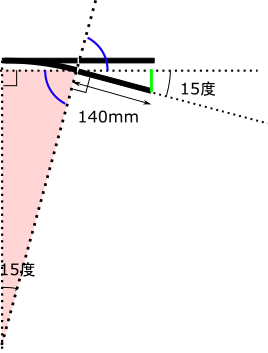
緑色の辺の長さを求められればOKで、15度の角度がついてますので、sin (15) を 140 にかければ求められます。青い部分の角度が同じですので、三角形の内角の和が180度ということを考えればポイントの分岐角度に等しくなりますね。
線路間の間隔に対して、長さはどうでしょうか?
以下のように、分岐側は直線側に対して約 5mm 短くなることが分かります。レイアウトプランなどでも S72.5 で長さを調整されているケースがありますが、2本連ねて直線側に合わせられることが分かります。

ヤードや駅などでは半径の大きなレールをよく使うと思いますが、レイアウトで使う角度の大きなカーブレールの場合はどうでしょうか。
以下は半径 280mm、角度 45度の場合です。レイアウト中にカーブレールを使ってS字を取り入れた場合にどう計算すれば良いでしょうか。基本は先ほどのケースと同じです。図中の x を求められれば 280 から引き算で L の長さが求められます。

実際に計算すると以下のようになります。
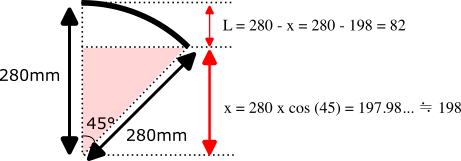
S字カーブを組む時は中間に直線レールを入れた方が脱線防止には良いです。
以下は S280 を入れた時のそれぞれのサイズを求めたものです。

こんな感じで半径や角度を実際に使用するレールに合わせて考えると、オリジナルのレイアウトでも寸法計算は大丈夫です。
また、複数のレールをつなぎ合わせていきますので、少しの差は誤差として吸収できます。公式のレイアウトプランでもわずかな誤差はあることもお分かりいただけたかと思います。Google検索も活用して学生時代三角関数とか数学苦手だった方も乗り越えていきましょう!好きなことに活用するとなれば苦手も克服です!
それでは皆様の鉄道模型ライフがより楽しくハッピーになりますように!






